ロジスティック回帰は、分類問題を解くための基本的な機械学習アルゴリズムの一つです。
名前に“回帰”とありますが、実際には分類タスクに使われるモデルであることをご存じでしょうか?
この記事では、E資格を目指す人にも役立つように、
- ロジスティック回帰の考え方
- 数式の意味と直感的な理解
- 実際にどんな場面で使えるのか
- メリット・デメリット
を、数式・図・例を使いながら、わかりやすく整理してお届けします!
AIに関する基本的な説明はこちらの記事で行なっています!
機械学習の分類とロジスティック回帰の位置づけ
機械学習は大きく分けて以下の3つのカテゴリーに分類されます。
教師あり学習
- 分類:データを特定のカテゴリに分類する(例:スパムメールの判定)
- 回帰:数値を予測する(例:住宅価格の予測)
教師なし学習
- クラスタリング:データを自然なグループに分ける(例:顧客のセグメンテーション)
- 異常検知:通常とは異なるデータを検出する(例:不正アクセスの検出)
強化学習
- エージェントが環境と相互作用しながら最適な行動を学習する(例:ゲームAI)
ロジスティック回帰は、教師あり学習の中でも「分類」に特化したアルゴリズムです。
ロジスティック回帰とは
ロジスティック回帰は、「回帰」という言葉がついていますが、ロジスティック回帰は確率を出力し、分類を行うモデルです。
入力データの線形結合を、シグモイド関数で変換することで、出力を0〜1の範囲に収めます。
単純パーセプトロンとシグモイド関数
ニューラルネットワークでは、各ノード(単純パーセプトロン)が線形結合を計算した後に、活性化関数を適用して出力を決定します。
ロジスティック回帰では、この活性化関数としてシグモイド関数が用いられます。この関数は、入力が大きくなると1に近づき、小さくなると0に近づくS字型の曲線を描きます。
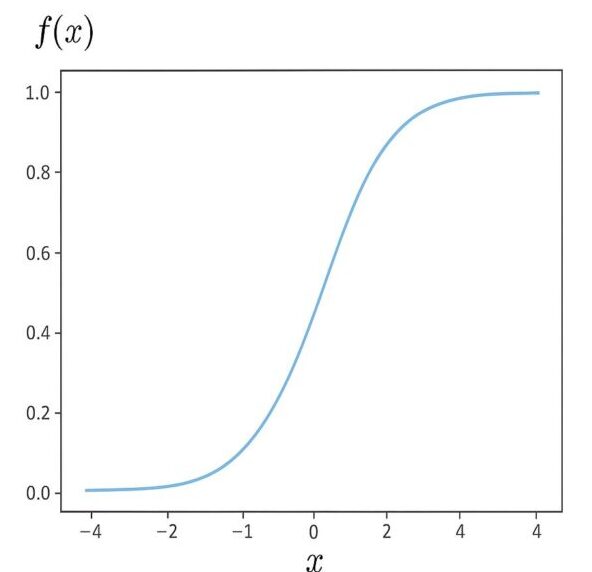
以下が計算の手順です⬇️
線形結合の計算
$$z=w_0 + w_1x_1 + \cdots + w_nx_n$$
これは、各特徴量xiに重みwiをかけて足し合わせたものです。数式の形が直線(線形)なので「線形結合」と呼ばれます。
シグモイド関数による変換
$$p=f(z) = \frac{1}{1 + e^{-z}}$$
ここで得られる pは、入力が特定のクラスに属する確率となります。具体的には、このように確率を出力し、その値がしきい値(例えば0.5)を超えるかどうかでクラス分けをします。
例:スパムメールの判定
| 確率(出力) | 分類結果 |
|---|---|
| 0.87 | スパム(1) |
| 0.21 | 非スパム(0) |
つまり、「確率を使った分類」というスタイルがロジスティック回帰の本質です。
オッズとロジットの理解
ロジスティック回帰では、確率をオッズに変換し、その対数(ロジット)を線形関数としてモデル化します。
オッズとロジットの定義
- オッズ:事象が起こる確率を、起こらない確率で割ったもの。
- ロジット:オッズの自然対数。
数式で表すと以下のようになります:
$$\text{オッズ} = \frac{p}{1 – p}$$
$$\text{ロジット}(p) = \log\left(\frac{p}{1 – p}\right) = w_0 + w_1 x_1 + \cdots + w_n x_n$$
このように、ロジスティック回帰はロジットを線形関数としてモデル化し、最終的にシグモイド関数を通じて確率を出力します。
ロジスティック回帰の利点と限界
メリット
- 解釈性の高さ:各特徴量の重みから、その影響度を理解しやすい。
- 計算効率:学習が比較的高速で、実装も容易。
- 過学習のリスクが低い:モデルがシンプルなため、過学習しにくい。
デメリット
- 線形分離できないデータには不向き:複雑な境界は表現できない
- 非線形性が必要なケースでは弱い: SVMのほうが有効な場合も要。
ロジスティック回帰はどんなときに使う?
具体的な応用例
- 顧客が商品を買うかどうかの予測
- 病気の有無の診断
- 離職リスクの判定
- 金融における信用リスクのスコアリング
注意:絶対にロジスティック回帰を使う、というわけではない!
機械学習においては「このタスクにはこの手法一択!」ということはほとんどありません。
実務では以下のような流れになります。
- ロジスティック回帰などベーシックな手法を試す
- 精度や再現率などを確認
- 必要に応じて決定木・ランダムフォレスト・SVM・深層学習など他のモデルも検討
つまり、「分類タスクではまずロジスティック回帰も候補に挙げる」というのが現場での常識的な立ち位置です。
まとめ
ロジスティック回帰は、分類問題を解決するための基本的かつ強力なアルゴリズムです。そのシンプルさと解釈性の高さから、多くの実践的な問題に適用されています。特に、特徴量と目的変数の関係が線形である場合に効果的です。
ちなみに私がE資格の認定プログラムを受講したのはここです!
👉 AI研究所 E資格対策講座(公式サイト)
勉強に使った教材はこちらです⬇️


